NMF 0.17.6

Using the main function nmf()


  
# generate a synthetic dataset with known classes: 50 features, 23 samples (10+5+8)
n <- 20; counts <- c(5, 3, 2);

p <- sum(counts)

x <- syntheticNMF(n, counts)

dim(x)



[1] 20 10

# build the true cluster membership
groups <- unlist(mapply(rep, seq(counts), counts))

# run on a data.frame
res <- nmf(data.frame(x), 3)

# missing method: use algorithm suitable for seed
res <- nmf(x, 2, seed=rnmf(2, x))

algorithm(res)



[1] "brunet"

res <- nmf(x, 2, seed=rnmf(2, x, model='NMFns'))

algorithm(res)



[1] "nsNMF"

# compare some NMF algorithms (tracking the approximation error)
res <- nmf(x, 2, list('brunet', 'lee', 'nsNMF'), .options='t')



Compute NMF method 'brunet' [1/3] ... OK
Compute NMF method 'lee' [2/3] ... OK
Compute NMF method 'nsNMF' [3/3] ... OK

res




Length: 3 
Method(s): brunet, lee, nsNMF 
Total timing:
   user  system elapsed 
  1.044   0.004   1.052 

summary(res, class=groups)



       method   seed rng    metric rank sparseness.basis sparseness.coef purity   entropy silhouette.coef silhouette.basis residuals niter
brunet brunet random   1        KL    2        0.2932845       0.8254661    0.7 0.4984430               1                1  67.54475   420
lee       lee random   1 euclidean    2        0.3725724       0.6479075    0.8 0.3063008               1                1  40.01078   450
nsNMF   nsNMF random   1        KL    2        0.3613243       0.9999992    0.7 0.4984430               1                1  71.77176   430
         cpu cpu.all nrun
brunet 0.112   0.112    1
lee    0.180   0.180    1
nsNMF  0.252   0.252    1

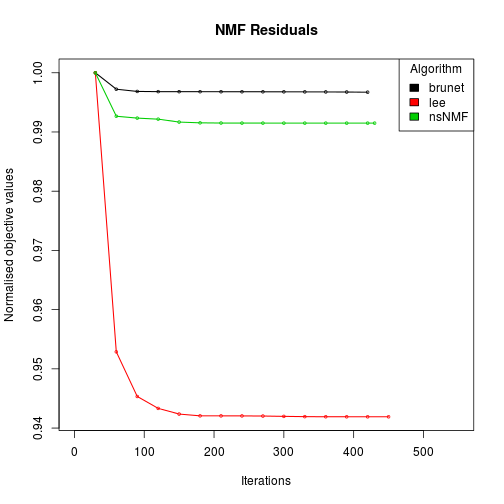
# plot the track of the residual errors
plot(res)

# specify algorithm by its name
res <- nmf(x, 3, 'nsNMF', seed=123) # nonsmooth NMF

# names are partially matched so this also works
identical(res, nmf(x, 3, 'ns', seed=123))



[1] FALSE

res <- nmf(x, 3, 'offset') # NMF with offset

# run a custom algorithm defined as a standard function
myfun <- function(x, start, alpha){
# update starting point
# ...
basis(start) <- 3 * basis(start)
# return updated point
start
}

res <- nmf(x, 2, myfun, alpha=3)

algorithm(res)



[1] "nmf_4a3f4f7c37e1"

# error: alpha missing
try( nmf(x, 2, myfun) )




 # Model:
  
  features: 20 
  basis/rank: 2 
  samples: 10 
 # Details:
  algorithm:  nmf_4a3f682621de 
  seed:  random 
  RNG: 403L, 111L, ..., 905346294L [32127b1f5d128e86611ca13100c4e072]
  distance metric:  'euclidean' 
  residuals:  93757.77 
  Timing:
     user  system elapsed 
    0.004   0.000   0.001 

# possibly the algorithm fits a non-standard NMF model, e.g. NMFns model
res <- nmf(x, 2, myfun, alpha=3, model='NMFns')

modelname(res)



[1] "NMFns"

# assume a known NMF model compatible with the matrix `x`
y <- rnmf(3, x)

# fits an NMF model (with default method) on some data using y as a starting point
res <- nmf(x, y)

# the fit can be reproduced using the same starting point
nmf.equal(nmf(x, y), res)



[1] TRUE

# missing method: use default algorithm
res <- nmf(x, 3)

# Fit a 3-rank model providing an initial value for the basis matrix
nmf(x, rmatrix(nrow(x), 3), 'snmf/r')




 # Model:
  
  features: 20 
  basis/rank: 3 
  samples: 10 
 # Details:
  algorithm:  snmf/r 
  seed:  NMF 
  RNG: 403L, 471L, ..., 905346294L [5b3bc938a22917243a2ad8c9fc79d83d]
  distance metric:   
  residuals:  32.96566 
  Iterations: 70 
  Timing:
     user  system elapsed 
    0.184   0.000   0.232 

# Fit a 3-rank model providing an initial value for the mixture coefficient matrix
nmf(x, rmatrix(3, ncol(x)), 'snmf/l')




 # Model:
  
  features: 20 
  basis/rank: 3 
  samples: 10 
 # Details:
  algorithm:  snmf/l 
  seed:  NMF 
  RNG: 403L, 515L, ..., 905346294L [a4cdbeabe17bc6669787b00b08588da7]
  distance metric:   
  residuals:  32.93398 
  Iterations: 65 
  Timing:
     user  system elapsed 
    0.168   0.000   0.168 

# default fit
res <- nmf(x, 2)

summary(res, class=groups)



            rank sparseness.basis  sparseness.coef           purity          entropy  silhouette.coef silhouette.basis        residuals 
       2.0000000        0.3836735        0.6690929        0.8000000        0.3811979        1.0000000        1.0000000       66.2048250 
           niter              cpu          cpu.all             nrun 
     450.0000000        0.1120000        0.1120000        1.0000000 

# run default algorithm multiple times (only keep the best fit)
res <- nmf(x, 3, nrun=10)

res




  Method: brunet 
  Runs:  10 
  RNG:
   407L, 735887289L, 356183078L, -363657105L, -463838236L, -682061419L, -2098846382L 
  Total timing:
   user  system elapsed 
  3.588   0.300   2.600 

summary(res, class=groups)



                rank     sparseness.basis      sparseness.coef               purity              entropy      silhouette.coef 
           3.0000000            0.4680864            0.7657260            0.9000000            0.1738140            0.9266244 
    silhouette.basis            residuals                niter                  cpu              cpu.all                 nrun 
           0.8109707           44.6115320          420.0000000            0.2200000            3.5880000           10.0000000 
          cophenetic           dispersion silhouette.consensus 
           0.9802005            0.7080000            0.7582481 

# run default algorithm multiple times keeping all the fits
res <- nmf(x, 3, nrun=10, .options='k')

res




  Method: brunet 
  Runs:  10 
  RNG:
   407L, 1017738740L, -1532700571L, 258173410L, -924957701L, 1735077632L, 1899471617L 
  Total timing:
   user  system elapsed 
  4.564   0.420   2.290 
  Sequential timing:
   user  system elapsed 
  1.840   0.008   1.859 

summary(res, class=groups)



                rank     sparseness.basis      sparseness.coef               purity              entropy      silhouette.coef 
           3.0000000            0.4681643            0.7694107            0.9000000            0.1738140            0.9071356 
    silhouette.basis            residuals                niter                  cpu              cpu.all                 nrun 
           0.7994680           44.6115286          430.0000000            0.1640000            4.5640000           10.0000000 
          cophenetic           dispersion silhouette.consensus 
           0.9847183            0.7840000            0.8386278 

## Note: one could have equivalently done
# res <- nmf(V, 3, nrun=10, .options=list(keep.all=TRUE))
# use a method that fit different model
res <- nmf(x, 2, 'nsNMF')

fit(res)




features: 20 
basis/rank: 2 
samples: 10 
theta: 0.5 

# pass parameter theta to the model via `...`
res <- nmf(x, 2, 'nsNMF', theta=0.2)

fit(res)




features: 20 
basis/rank: 2 
samples: 10 
theta: 0.2 

## handling arguments in `...` and model parameters
myfun <- function(x, start, theta=100){ cat("theta in myfun=", theta, "\n\n"); start }

# no conflict: default theta
fit( nmf(x, 2, myfun) )



theta in myfun= 100 





features: 20 
basis/rank: 2 
samples: 10 

# no conlfict: theta is passed to the algorithm
fit( nmf(x, 2, myfun, theta=1) )



theta in myfun= 1 





features: 20 
basis/rank: 2 
samples: 10 

# conflict: theta is used as model parameter
fit( nmf(x, 2, myfun, model='NMFns', theta=0.1) )



theta in myfun= 100 





features: 20 
basis/rank: 2 
samples: 10 
theta: 0.1 

# conflict solved: can pass different theta to model and algorithm
fit( nmf(x, 2, myfun, model=list('NMFns', theta=0.1), theta=5) )



theta in myfun= 5 





features: 20 
basis/rank: 2 
samples: 10 
theta: 0.1 

## USING SEEDING METHODS
# run default algorithm with the Non-negative Double SVD seeding method ('nndsvd')
res <- nmf(x, 3, seed='nndsvd')

## Note: partial match also works
identical(res, nmf(x, 3, seed='nn'))



[1] FALSE

# run nsNMF algorithm, fixing the seed of the random number generator
res <- nmf(x, 3, 'nsNMF', seed=123456)

nmf.equal(nmf(x, 3, 'nsNMF', seed=123456), res)



[1] TRUE

# run default algorithm specifying the starting point following the NMF standard model
start.std <- nmfModel(W=matrix(0.5, n, 3), H=matrix(0.2, 3, p))

nmf(x, start.std)




 # Model:
  
  features: 20 
  basis/rank: 3 
  samples: 10 
 # Details:
  algorithm:  brunet 
  seed:  NMF 
  RNG: 403L, 342L, ..., 1047588911L [8ed89da992168bfe13a600ef97943baa]
  distance metric:  'KL' 
  residuals:  89.23127 
  Iterations: 420 
  Timing:
     user  system elapsed 
    0.104   0.000   0.105 

# to run nsNMF algorithm with an explicit starting point, this one
# needs to follow the 'NMFns' model:
start.ns <- nmfModel(model='NMFns', W=matrix(0.5, n, 3), H=matrix(0.2, 3, p))

nmf(x, start.ns)




 # Model:
  
  features: 20 
  basis/rank: 3 
  samples: 10 
  theta: 0.5 
 # Details:
  algorithm:  nsNMF 
  seed:  NMF 
  RNG: 403L, 342L, ..., 1047588911L [8ed89da992168bfe13a600ef97943baa]
  distance metric:  'KL' 
  residuals:  89.23127 
  Iterations: 420 
  Timing:
     user  system elapsed 
    0.220   0.004   0.222 

# Note: the method name does not need to be specified as it is infered from the
# when there is only one algorithm defined for the model.
# if the model is not appropriate (as defined by the algorihtm) an error is thrown
# [cf. the standard model doesn't include a smoothing parameter used in nsNMF]
try( nmf(x, start.std, method='nsNMF') )

## Callback functions
# Pass a callback function to only save summary measure of each run
res <- nmf(x, 3, nrun=3, .callback=summary)

# the callback results are simplified into a matrix
res$.callback



                        [,1]        [,2]        [,3]
rank               3.0000000   3.0000000   3.0000000
sparseness.basis   0.4690227   0.4646504   0.4580022
sparseness.coef    0.8045101   0.7769446   0.8068001
silhouette.coef    0.9546248   0.8902991   0.8762803
silhouette.basis   0.8394310   0.7919504   0.7687868
residuals         44.6117396  44.6136628  45.3878071
niter            450.0000000 430.0000000 860.0000000
cpu                0.2000000   0.1320000   0.2920000
cpu.all            0.2000000   0.1320000   0.2920000
nrun               1.0000000   1.0000000   1.0000000

res <- nmf(x, 3, nrun=3, .callback=summary, .opt='-S')

# the callback results are simplified into a matrix
res$.callback



[[1]]
            rank sparseness.basis  sparseness.coef  silhouette.coef silhouette.basis        residuals            niter              cpu 
       3.0000000        0.3608160        0.8514485        0.9150132        0.7120422       50.4900252      480.0000000        0.1480000 
         cpu.all             nrun 
       0.1480000        1.0000000 

[[2]]
            rank sparseness.basis  sparseness.coef  silhouette.coef silhouette.basis        residuals            niter              cpu 
       3.0000000        0.4684599        0.7880077        0.9424514        0.8147630       44.6115438      420.0000000        0.1920000 
         cpu.all             nrun 
       0.1920000        1.0000000 

[[3]]
            rank sparseness.basis  sparseness.coef  silhouette.coef silhouette.basis        residuals            niter              cpu 
       3.0000000        0.4649104        0.8032040        0.9475480        0.8329278       44.6134353      440.0000000        0.1720000 
         cpu.all             nrun 
       0.1720000        1.0000000 


# Pass a custom callback function
cb <- function(obj, i){ if( i %% 2 ) sparseness(obj) >= 0.5 }

res <- nmf(x, 3, nrun=3, .callback=cb)

res$.callback



[[1]]
basis  coef 
FALSE  TRUE 

[[2]]
NULL

[[3]]
basis  coef 
FALSE  TRUE 


# Passs a callback function which throws an error
cb <- function(){ i<-0; function(object){ i <<- i+1; if( i == 1 ) stop('SOME BIG ERROR'); summary(object) }}

res <- nmf(x, 3, nrun=3, .callback=cb())


Warning message:
NMF::nmf - All NMF fits were successful but 3/3 callback call(s) threw an error.
# Callback error(s) thrown:
  - run #1: SOME BIG ERROR
## PARALLEL COMPUTATIONS
# try using 3 cores, but use sequential if not possible
res <- nmf(x, 3, nrun=3, .options='p3')

# force using 3 cores, error if not possible
res <- nmf(x, 3, nrun=3, .options='P3')

# use externally defined cluster
library(parallel)

cl <- makeCluster(6)

res <- nmf(x, 3, nrun=3, .pbackend=cl)

# use externally registered backend
registerDoParallel(cl)

res <- nmf(x, 3, nrun=3, .pbackend=NULL)